√画像をダウンロード 四 ���錐 台 体積 461338-四角錐台体積 公式
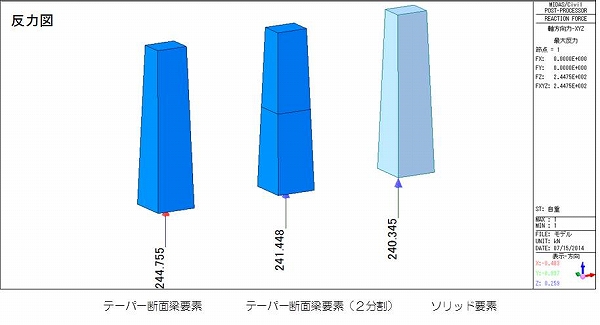
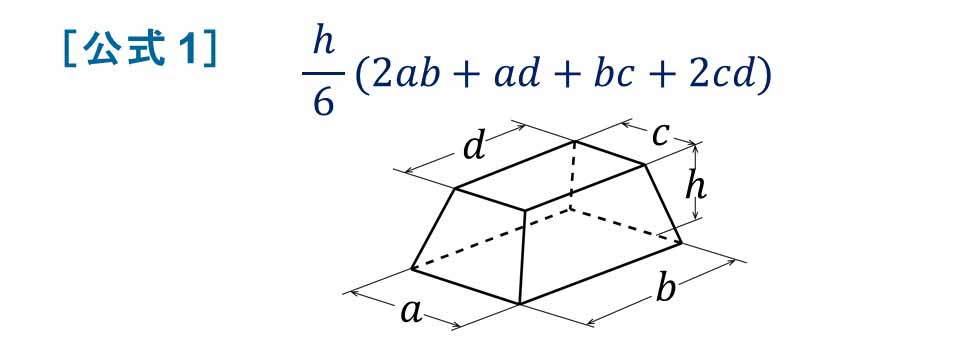
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体積への拡張 一応最初なので、シンプソンの公
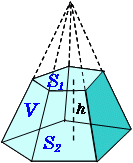
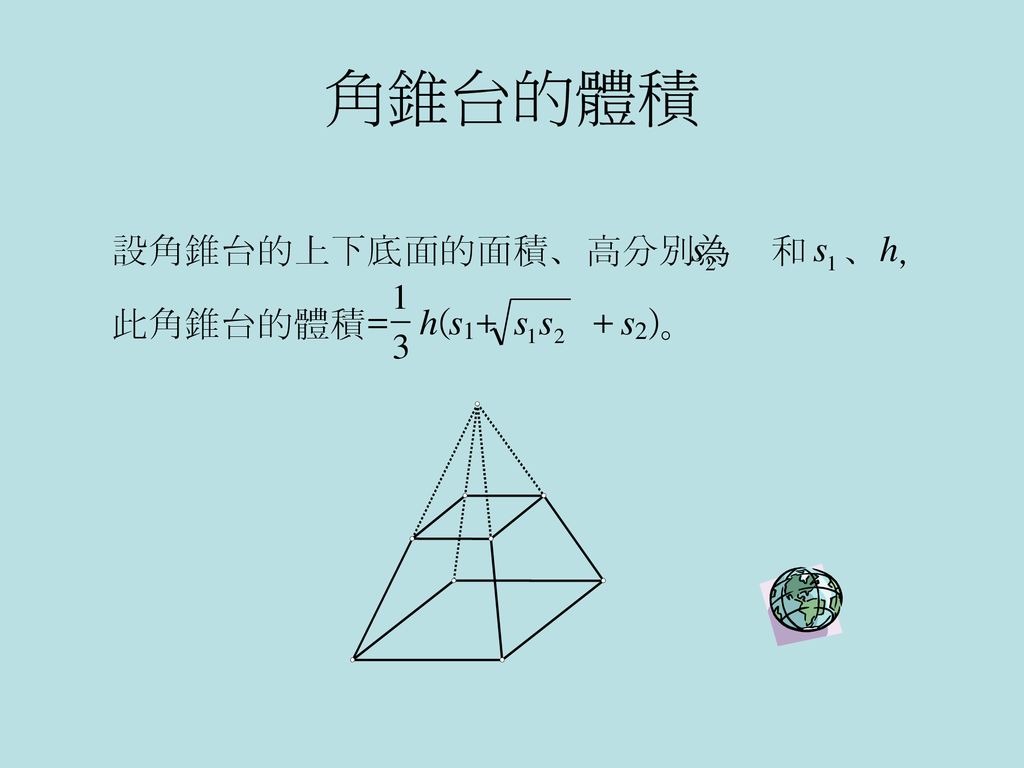
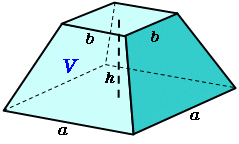
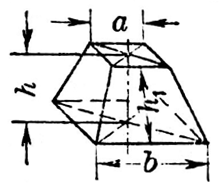
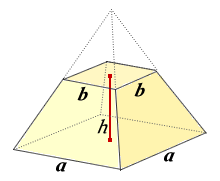
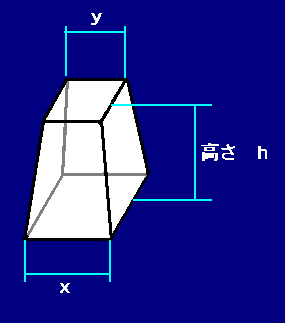
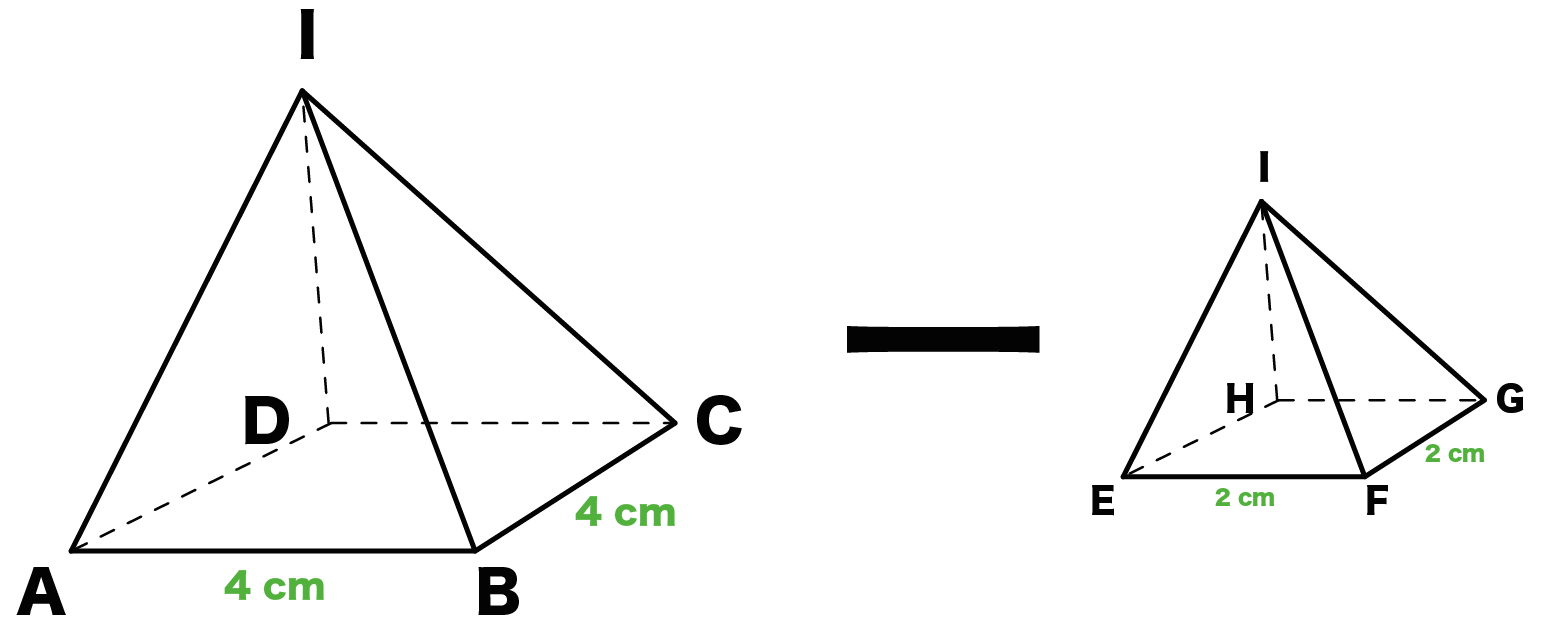
四角錐台体積 公式- 底面が一辺 2 h 2h 2 h の正方形であるような特殊な正四角錐の場合は，立方体を六個に切ることで簡単に V = 1 3 S h V=\dfrac{1}{3} Sh V = 3 1 S h が証明できます。 証明 底面積は S = 4 h 2 S=4h^2 S = 4 h 2 高さは h h h また，一辺 2 h 2h 2 h の立方体から同じ形の立体が六個取り出せるので，体積は (2 h) 3 ÷ 6 = 4 3四角すいの体積 A： B： H： 体積： 球 球 半球 中空球 円周から体積 円柱 円柱 パイプ 円周から体積 立方体 立方体・直方体 角パイプ 錐体 円すい 四角すい 多角形 6
四角錐台体積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 | -%E6%95%B8%E5%AD%B84A/20210325_100250_0014.jpg "龍騰高中月考王評量2年級 下 數學4a 崇善網路書店 專注於網路參考書升學書籍專賣") | |
 |  | |
「四角錐台体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「四角錐台体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「四角錐台体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  | |
「四角錐台体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  |  |
「四角錐台体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「四角錐台体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  |  |
「四角錐台体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「四角錐台体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |
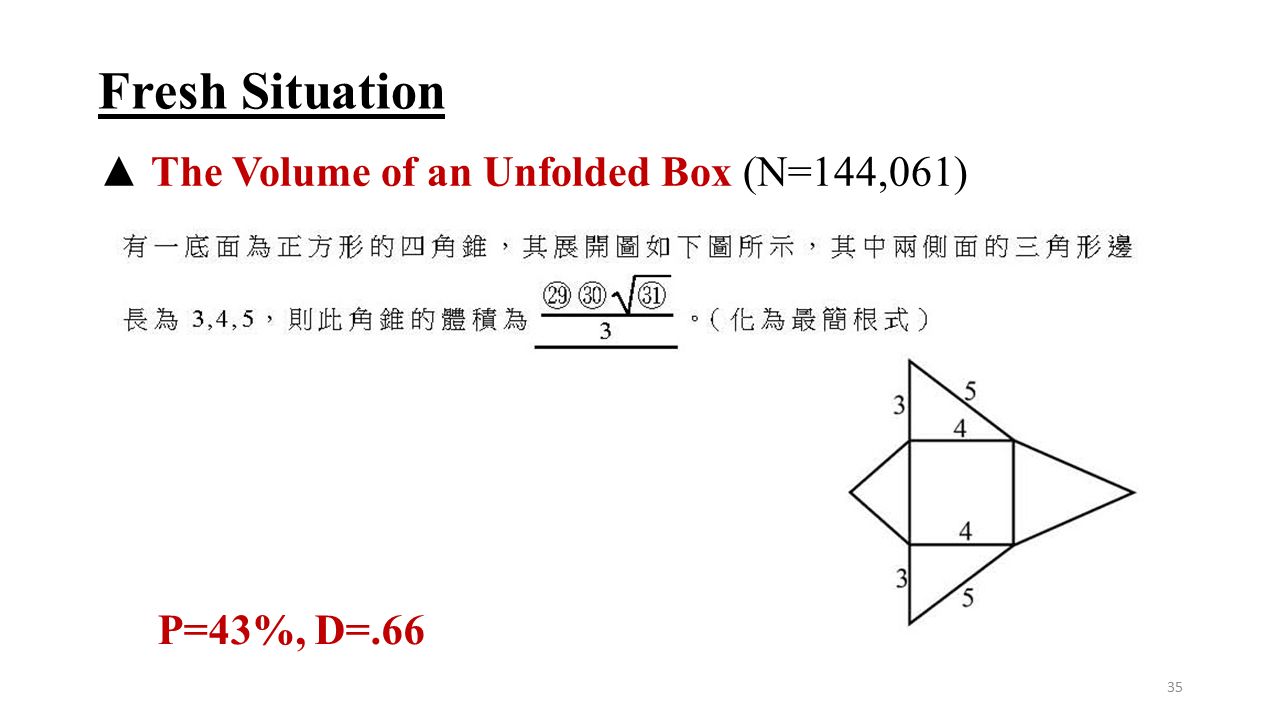
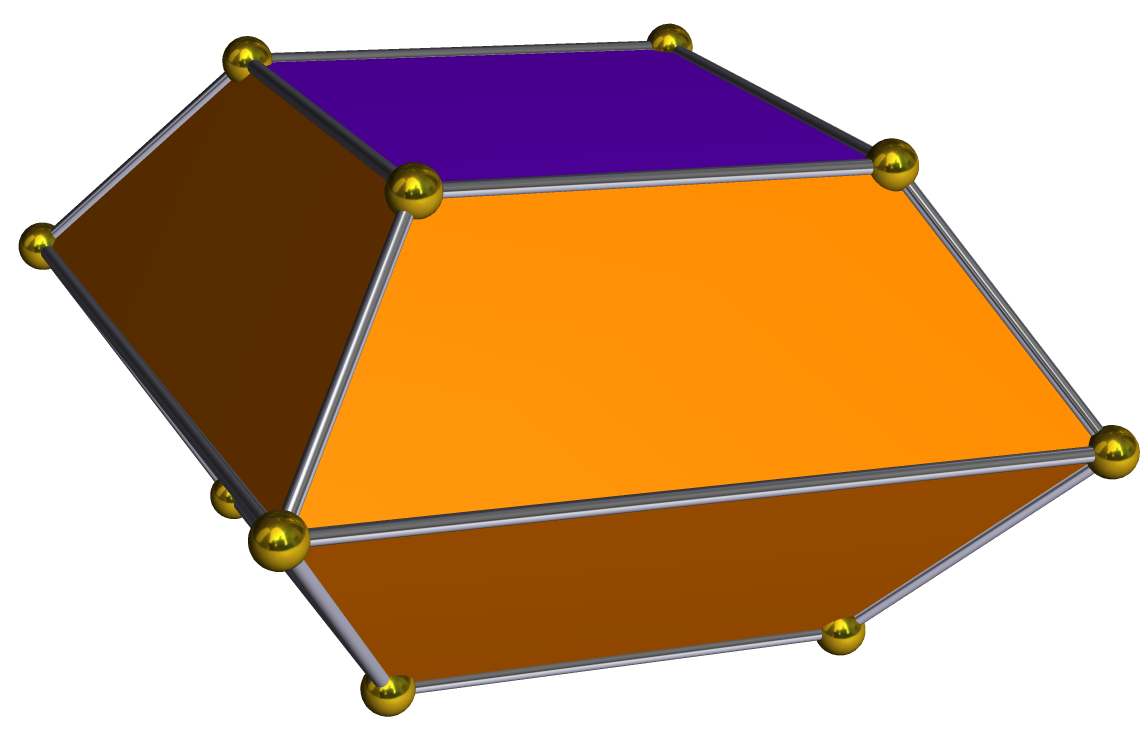
ちなみに、立体をなす平面の数に注目すると、三角錐は「四面体」と呼ぶこともできます（計 \(4\) 面で構成されているため）。 特殊な三角錐：「正三角錐」と「正四面体」 底面が正三角形で、側面がすべて合同な二等辺三角形で作られた三角錐を「正三角錐」といいます。 また、すべてのJohnson多面體 编辑 在 Johnson多面體 當中J 1 是一個以 正方形 為底並和其它四個 正三角形 所構成的四角錐，是Johnson多面體中構造最簡單的一個，形似 金字塔 。 同時它也是 柏拉圖立體 中 正八面體 的一半 。 最早在1966年首先被 諾曼·詹森 （英语：Norman Johnson (mathematician)） 命名和描述。 J 1 共有8個邊、5個面、5個 頂點 。 若設其一邊為 ， 體積 為 ， 高 為 ，則：
Incoming Term: 四角錐台体積 公式,
コメント
コメントを投稿